For nearly three full centuries, the most accurate way that humanity kept track of time was through the pendulum clock. From its initial development in the 17th century until the invention of quartz timepieces in the 1920s, pendulum clocks became staples of household life, enabling people to organize their schedules according to a universally agreed upon standard. Initially invented in the Netherlands by Christian Huygens all the way back in 1656, their early designs were quickly refined to greatly increase their precision, where it soon became routine for pendulum clocks to keep time accurately to within a tolerance of just ~2 seconds per day.
But when the first pendulum clock was brought to the Americas, something bizarre happened. The clock, which had worked perfectly well at keeping accurate time in Europe, was initially synchronized with known astronomical phenomena, like sunset/sunrise and moonset/moonrise. But after only a week or two in the Americas, it was clear that the clock wasn’t keeping time properly. The first clock in America was a complete failure, but that’s only the beginning of a story that would revolutionize our understanding of the physics of, and gravitation on, planet Earth.
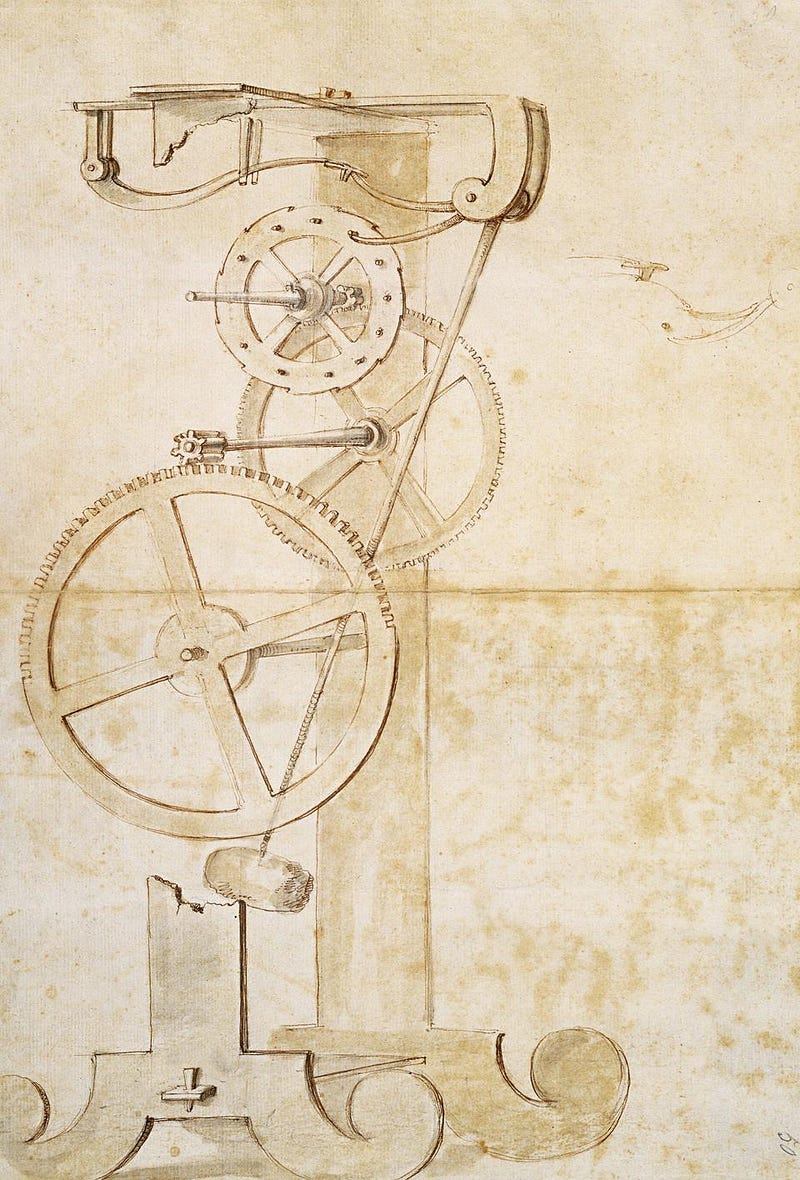
For thousands of years, scientists had no better method for keeping time than the ancient sundial. But starting in the early 1600s, scientific investigations into the swinging pendulum — and, in particular, Galileo’s observation that the period of a pendulum was determined solely by its length — led to the idea that a pendulum could theoretically be used as a clock. It wouldn’t depend on the thickness of the pendulum itself, the mass of the weight at the end of it, or on the angle to which the pendulum was raised; only the length of the pendulum mattered for its period. Galileo discussed the idea in 1637, and although he died in 1642, the idea would not only live on, but would influence a generation of scientists just coming into their own.
In 1656, working in the Netherlands, Christiaan Huygens invented the very first working pendulum clock, which was both primitive and revolutionary in a number of ways. Over the next few decades, refinements were made that improved the pendulum clock even further, including:
- shortening the swing so that it would only swing through narrow, small angles, increasing its accuracy,
- increasing the length of the pendulum and putting a heavy mass on the end, which increased the clock’s longevity,
- standardizing a length of 0.994 meters for the pendulum, which meant that each “swing” from one side to the other lasted exactly one second (a “seconds pendulum”),
- and the addition of a minute hand, as the clocks were now accurate enough so that fractions of an hour, down to the minute, were now meaningful quantities to discuss.

All of these innovations had been made prior to 1700: a remarkable set of advances in a short amount of time. The largest remaining “source of error” that occurred with these pendulum clocks was due to temperature changes: the length of the pendulum would increase or decrease as the materials they were made out of thermally expanded or contracted in a temperature-dependent way. By developing a temperature-compensated pendulum — where the period of a swing didn’t change even as the temperature did — pendulum clocks could be accurate to within just a few seconds per week. The first American-built clock wouldn’t occur for many decades after that advance, and so the first attempts to keep time in the Americas would rely on devices that were imported from Europe.
This is where the big puzzle of timekeeping arose: when the first pendulum clock was brought from Europe to America. The clock, built and calibrated in the Netherlands, was exquisitely accurate. Sunset/sunrise and moonset/moonrise times were accurate for weeks, with stars rising and setting within a minute of the predicted time without any need for further calibration until approximately a full month had passed.
But upon arriving in America, the clock was wound, began ticking, and in very short order, everything began to go wrong.
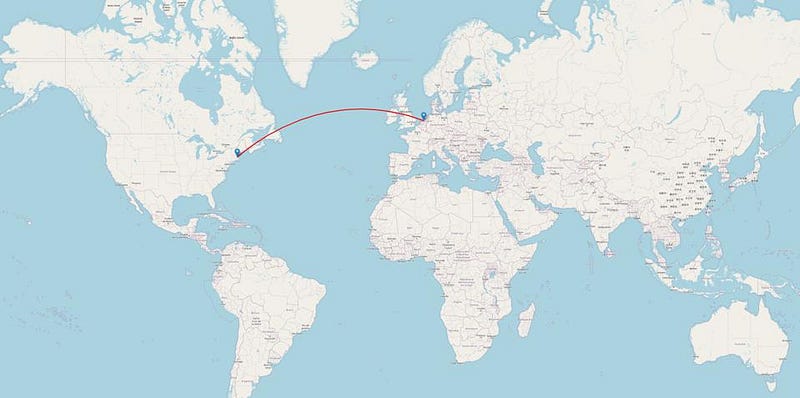
Within a single week, people noticed that the Sun and Moon weren’t rising or setting at the predicted times, according to this new clock. Moreover, the mismatch was getting worse with each passing day. Whereas the clock was supposed to be accurate — at the time — to within about 2 seconds per day, or about 15 seconds per week, it was observed to be running slow by more than 30 seconds per day. By the end of the first week, it was off by about 4-to-5 minutes, a woefully unacceptable error.
Clearly, they concluded, the clock must have suffered some damage during the trans-Atlantic journey that brought the clock from Europe to the Americas. So they did the only thing they knew how to do: they sent the clock back to the manufacturer for repair. After another trans-Atlantic journey, the clock was returned to the Netherlands from the Americas. When it arrived, they wound the clock, observed its ticking, and compared it to all the other ways they knew of keeping time: to other clocks, to sundials, and to the rising and setting of celestial objects.
Despite the observations of poor timekeeping in the Americas, when the clock was properly set up in Europe once again, it kept time to within 2 seconds per day. In other words, the clock appeared to be perfectly accurate.
This maddening experience is familiar to anyone who’s ever been in a scenario where your car is doing something you know it shouldn’t be doing: making a funny sound, handling improperly, getting too hot, etc. You notice the problem, you take it to a mechanic, and as soon as you arrive at the mechanic, the car starts behaving as though nothing is wrong. The omnipresent problem that you’ve been experiencing constantly suddenly resolves itself when you arrive at the one person who could diagnose and fix it. Yet, as soon as you drive away, it inevitably starts having that problem again. That same maddening experience, and that same helpless feeling, affected those seeking to keep time in America more than 300 years ago
If the European manufacturer had then sent that clock back to the Americas, they would have experienced exactly the same phenomenon once again. The clock — which kept exquisitely accurate time in Europe — would have begun running at the wrong rate in the Americas once again. The reason would have been totally obscure to anyone living in the time of Galileo, but it began to make sense once we started to understand how gravitation worked.
Here on Earth, the gravitational force is what drives the swinging of a pendulum. If you move a pendulum just a little bit away from its equilibrium position, the force of gravity is what pulls it back toward the equilibrium position. It’s true that the period of the pendulum is related to the length of the pendulum: if you want to double the period, you need to quadruple the length. (A pendulum that’s 0.994 meters long will take two seconds to return to its starting position; a pendulum that’s 0.2485 meters long will take 1 second to return to its starting position; one that’s 3.974 meters long will take 4 seconds to return to its starting position, etc.)
But we wrongly assumed, before Newton came along, that gravity worked the same way everywhere on the surface of the Earth: that the acceleration due to gravity would have the exact same magnitude everywhere across Earth’s surface. Instead, gravitation works by attracting you toward the center of the Earth, even as the entire mass of the planet attracts you. Because the Earth spins on its axis, it bulges at its equator and gets compressed at the poles. The effect is slight but still substantial, causing Earth’s shape to be an oblate spheroid rather than a perfect sphere. And, from the perspective of gravitation, it means that someone at one of Earth’s poles (or at high latitudes) is therefore closer to the center of the Earth than someone at the equator (or at low latitudes).

If you’ve ever taken a physics class, you might have learned that all objects accelerate “downward” at 9.8 m/s² under the influence of gravity, meaning that if you drop an object from rest and neglect air resistance, then it will speed up, in the downward direction, by an additional 9.8 m/s (about 32 feet per second) for every second that elapses while it falls.
And that’s true! Anywhere you go, on the surface of Earth, you’ll observe that same acceleration downward, toward Earth’s center: at a rate of 9.8 m/s².
But it’s not still true if you go to the third significant figure: to what’s commonly cited as 9.81 m/s². At the poles, where you’re closest to Earth’s center, the gravitational acceleration is a little bit larger than average: 9.83 m/s². At the equator, where you’re farthest from Earth’s center, the gravitational acceleration is a bit smaller than average: 9.78 m/s². And there’s a gradient there: these changes occur gradually from the pole to the equator and back to the opposite pole once again. Although these effects are tiny, they’re cumulative. And therefore, over enough time, they’ll add up to be quite significant.
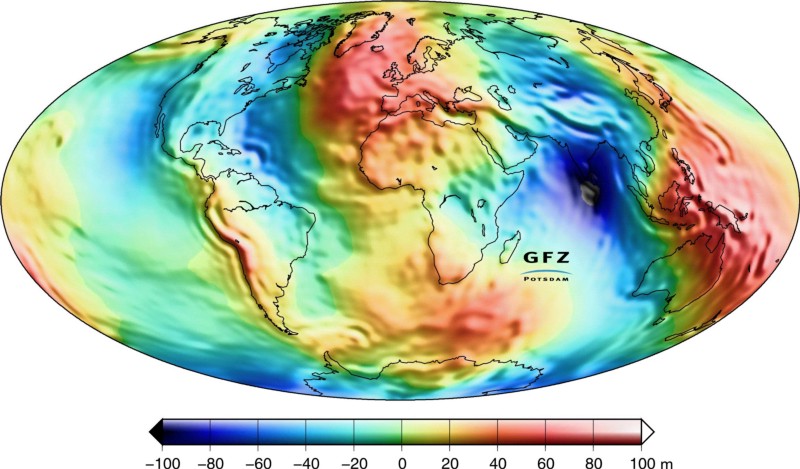
Although we think of the most populated areas of Europe and North America to be at roughly the same “mid-latitudes” as one another, that’s not quite the case. Amsterdam, the most populous city in the Netherlands, is at 52° N latitude. Boston, which was the most northern large city in the Americas in the late 1600s/early 1700s, is a full 10° farther south: at 42° N latitude. Other major population centers in the Americas at that same time, like New York, Philadelphia, or Jamestown, were even further south, closer to the equator, exacerbating the difference between the gravity experienced by Europeans and Americans.
Elevation changes can also make a difference, with lowland locations near the poles having the highest accelerations on Earth: up to a maximum recorded value of 9.834 m/s², while high mountain ranges near the equator lead to the lowest measured accelerations: 9.764 m/s². However, the latitude problem is particularly important when it comes to timekeeping, and we can recognize this for ourselves just by performing a relatively simple calculation.
Let’s imagine that we’ve built a pendulum clock where the pendulum is exactly 0.994 meters in length: what’s known as a seconds pendulum. Each half-swing of the pendulum should take precisely 1 second, and since we know that there are 86,400 seconds in a 24 hour day, we know — in theory — how to measure a day: just divide 86,400 by 2, and that gives you 43,200. Measuring that many full swings of your seconds pendulum, a full 43,200 of them, should add up to one full day, or 86,400 seconds.
Here’s how well we’d do by measuring 43,200 swings of this pendulum, depending on our local value of Earth’s acceleration, the parameter known as g:
- g = 9.83 m/s²: clock runs 1 minute 26 seconds fast, per day,
- g = 9.82 m/s²: clock runs 42 seconds fast, per day,
- g = 9.81 m/s²: clock runs 2 seconds slow, per day,
- g = 9.80 m/s²: clock runs 46 seconds slow, per day,
- g = 9.79 m/s²: clock runs 1 minute 30 seconds slow, per day,
- and g = 9.78 m/s²: the clock runs 2 minutes 14 seconds slow, per day.
Properly calibrating a pendulum clock — as we now know — doesn’t just involve setting the length equal to a particular value; it means ensuring that the pendulum has the proper length for the gravitational acceleration at its particular location.
The pendulum clock, arguably, was the first experimental indication we had that gravity is not uniform over the surface of the Earth. Even before the advances of Isaac Newton, it was known that a pendulum — if the swing is small, the air resistance is negligible, and the temperature and length remain constant — always takes the same amount of time to complete a full swing. But the time it takes a pendulum to swing does vary over the surface of Earth, not only with length, but with two other factors: altitude and latitude, which determine your true distance from the gravitational center of the Earth.
It was a major hint toward a fact that we now take for granted: that the gravitational attraction from Earth depends on your distance to our planet’s center, rather than being uniform over the entire surface. The fact that the Earth rotates on its axis, and that rotation causes the equator to bulge compared to the poles, means that a pendulum takes longer to complete an oscillation as gravity gets weaker. Any pendulum clock, therefore, must be calibrated to the gravitational field of exactly where you are. The first clock in the Americas was a spectacular demonstration of this effect, with the underlying cause being the law of gravity itself!
This article was reprinted with permission of Big Think, where it was originally published.






